Hidden variable theory

Quantum mechanics
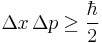\Delta x\, \Delta p \ge \frac{\hbar}{2}
Introduction
Glossary · History
Interpretations
Consciousness-caused
Consistent histories
Copenhagen · de Broglie–Bohm
Ensemble · Hidden variables
Many-worlds · Objective collapse
Pondicherry · Quantum logic
Relational · Stochastic
Transactional

Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation. Albert Einstein, the most famous proponent of hidden variables, famously insisted that, "I am convinced God does not play dice",[1] but whether he objected to the statistical nature of quantum mechanics is disputed.[2] Einstein, Podolsky, and Rosen argued that "elements of reality" (hidden variables) must be added to quantum mechanics to explain entanglement without action at a distance.[3][4] Later, Bell's theorem would suggest (in the opinion of most physicists and contrary to Einstein's assertion) that local hidden variables are impossible.

The most famous such theory (because it gives the same answers as quantum mechanics, thus invalidating the famous theorem by von Neumann that no hidden variable theory reproducing the statistical predictions of QM is possible) is that of David Bohm. It is most commonly known as the Bohm interpretation or the Causal Interpretation of quantum mechanics. In Bohm's interpretation, the (nonlocal) quantum potential constitutes an implicate (hidden) order, and may itself be the result of yet a further implicate order (superimplicate order).[5] Nowadays Bohm's theory is considered to be one of many interpretations of quantum mechanics which give a realist interpretation, and not merely a positivistic one, to quantum-mechanical calculations. By some it is considered the simplest theory to explain the orthodox quantum mechanics formalism.[6] Nevertheless it is a hidden variable theory.

The major reference for Bohm's theory today is his posthumous book with Basil Hiley.[7]

Contents

Motivation

Under the Copenhagen interpretation, quantum mechanics is nondeterministic, meaning that it generally does not predict the outcome of any measurement with certainty. Instead, it tells us what the probabilities of the outcomes are. This leads to the situation where measurements of a certain property done on two apparently identical systems can give different answers. The question arises whether there might be some deeper reality hidden beneath quantum mechanics, to be described by a more fundamental theory that can always predict the outcome of each measurement with certainty. In other words if the exact properties of every subatomic particle and smaller were known the entire system could be modeled exactly using deterministic physics similar to classical physics.

In other words, the Copenhagen interpretation of quantum mechanics might be an incomplete description of reality. Physicists supporting the Bohmian interpretation of quantum mechanics maintain that underlying the probabilistic nature of the universe is an objective foundation/property — the hidden variable. Others, however, believe that there is no deeper reality in quantum mechanics — experiments have shown a vast class of hidden variable theories to be incompatible with observations. Kirchmair and colleagues show that, in a system of trapped ions, quantum mechanics conflicts with hidden variable theories regardless of the quantum state of the system.[8]

Although determinism was initially a major motivation for physicists looking for hidden variable theories, nondeterministic theories trying to explain what the supposed reality underlying the quantum mechanics formalism looks like are also considered hidden variable theories; for example Edward Nelson's stochastic mechanics.

EPR Paradox & Bell's Theorem

In 1935, Einstein, Podolsky and Rosen wrote a four-page paper titled "Can quantum-mechanical description of physical reality be considered complete?" that argued that such a theory was in fact necessary, proposing the EPR Paradox as proof. In 1964, John Bell showed through his famous theorem that if local hidden variables exist, certain experiments could be performed where the result would satisfy a Bell inequality. If, on the other hand, Quantum entanglement is correct the Bell inequality would be violated. Another no-go theorem concerning hidden variable theories is the Kochen-Specker theorem.

Physicists such as Alain Aspect and Paul Kwiat have performed experiments that have found violations of these inequalities up to 242 standard deviations[9](excellent scientific certainty). This rules out local hidden variable theories, but does not rule out non-local ones (which would refute quantum entanglement). Theoretically, there could be experimental problems that affect the validity of the experimental findings.

Non-local hidden-variable theory

Assuming the validity of Bell's theorem, any classical hidden-variable theory which is consistent with quantum mechanics would have to be non-local, maintaining the existence of instantaneous or faster-than-light acausal relations (correlations) between physically separated entities. The first hidden-variable theory was the pilot wave theory of Louis de Broglie, dating from 1927. The currently best-known hidden-variable theory, the Causal Interpretation, of the physicist and philosopher David Bohm, created in 1952, is a non-local hidden variable theory. Those who believe the Bohm interpretation to be actually true (rather than a mere model or interpretation), and the quantum potential to be real, refer to Bohmian mechanics.

What Bohm did, unknowingly rediscovering (and extending) the idea that Louis de Broglie had proposed and abandoned, was to posit both the quantum particle, e.g. an electron, and a hidden 'guiding wave' that governs its motion. Thus, in this theory electrons are quite clearly particles. When you perform a double-slit experiment (see wave-particle duality), they go through one slit rather than the other. However, their choice of slit is not random but is governed by the guiding wave, resulting in the wave pattern that is observed.

Such a view does not contradict the idea of local events that is used in both classical atomism and relativity theory as Bohm's theory (and indeed quantum mechanics, with which it is exactly equivalent) are still locally causal but allow nonlocal correlations (that is information travel is still restricted to the speed of light). It points to a view of a more holistic, mutually interpenetrating and interacting world. Indeed Bohm himself stressed the holistic aspect of quantum theory in his later years, when he became interested in the ideas of Jiddu Krishnamurti. Nevertheless this nonlocality is seen as a weakness of Bohm's theory by some physicists.

Another possible weakness of Bohm's theory is that some, feel that it looks contrived. (Indeed, Bohm thought this of his original formulation of the theory.[10]) It was deliberately designed to give predictions which are in all details identical to conventional quantum mechanics.[10] Bohm's aim was not to make a serious counterproposal but simply to demonstrate that hidden-variable theories are indeed possible.[10] His hope was that this could lead to new insights and experiments that would lead beyond the current quantum theories.[10]

Gerard 't Hooft has disputed the validity of Bell's theorem on the basis of the superdeterminism loophole and proposed some ideas to construct local deterministic models.[11]

In August 2011, Roger Colbeck and Renato Renner published a proof that any extension of quantum mechanical theory, whether using hidden variables or otherwise, cannot provide a more accurate description of outcomes, assuming that observers have free will.[12]

References

  1. ^ private letter to Max Born, 4 December 1926, Albert Einstein Archives reel 8, item 180
  2. ^ J. S. Bell, Bertlmann's socks and the nature of reality, Epistemological Letters, Feb. 1977, reprinted as Chapter 12 of J. S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press 1987), p. 144.
  3. ^ Einstein, A.; Podolsky, B.; Rosen, N. (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Physical Review 47 (10): 777–780. Bibcode 1935PhRv...47..777E. doi:10.1103/PhysRev.47.777. 
  4. ^ "The debate whether Quantum Mechanics is a complete theory and probabilities have a non-epistemic character (i.e. nature is intrinsically probabilistic) or whether it is a statistical approximation of a deterministic theory and probabilities are due to our ignorance of some parameters (i.e. they are epistemic) dates to the beginning of the theory itself." See: arXiv:quant-ph/0701071v1 12 Jan 2007
  5. ^ David Pratt: David Bohm and the Implicate Order. Appeared in: Sunrise magazine, February/March 1993, Theosophical University Press
  6. ^ Michael K.-H. Kiessling: Misleading Signposts Along the de Broglie-Bohm Road to Quantum Mechanics, Foundations of Physics, volume 40, number 4, 2010, pp. 418-429 (abstract)
  7. ^ D.Bohm and B.J.Hiley, The Undivided Universe, Routledge, 1993, ISBN 0-415-06588-7.
  8. ^ Kirchmair, G., et al. (2009). "State-independent experimental test of quantum contextuality". Nature 460 (7254): 494–497. Bibcode 2009Natur.460..494K. doi:10.1038/nature08172. 
  9. ^ Kwiat, P. G., et al. (1999) Ultrabright source of polarization-entangled photons, Physical Review A 60, R773-R776
  10. ^ a b c d David Bohm (1957). Causality and Chance in Modern Physics. Routledge & Kegan Paul and D. Van Nostrand. p. 110. ISBN 0-8122-1002-6. 
  11. ^ G 't Hooft, The Free-Will Postulate in Quantum Mechanics [1]; Entangled quantum states in a local deterministic theory [2]
  12. ^ Roger Colbeck; Renato Renner (2011). "No extension of quantum theory can have improved predictive power". Nature Communications 2 (8).  Colbeck and Renner write: "In the present work, we have ... excluded the possibility that any extension of quantum theory (not necessarily in the form of local hidden variables) can help predict the outcomes of any measurement on any quantum state. In this sense, we show the following: under the assumption that measurement settings can be chosen freely, quantum theory really is complete."

Bibliography

See also